Как-то в беседе с Александой Алешковой на свет появилась простенькая задачка, на которой достаточно легко и наглядно можно показать такой инструмент как балансировочная таблица. В моем понимании балансировочная таблица — это электронная таблица, в которой можно формулами увязать между собой множество переменных, оставив некоторые из них в роли “вентилей”, “вращая” которые, можно привести систему взаимосвязанных переменных к интересующим нас значениям.
Лично я частенько прибегаю к созданию балансировочных таблиц как вспомогательному инструменту, позволяющему системно взглянуть на игру, выявить и устранить доминантные стратегии. На приведенном ниже примере можно освоить принцип построения подобных таблиц.
Условия задачи
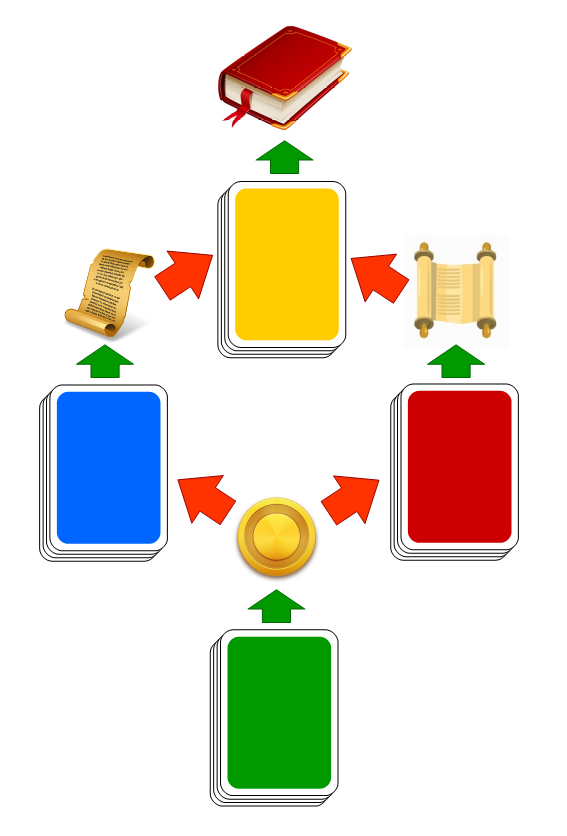
Представим, что у нас есть игра-викторина, в которой несколько игроков или команд, последовательно получают право взять одну случайную карточку с вопросом из колоды. Ответив верно на вопрос в карточке, команда получает награду. Побеждает игрок или команда, имеющая наибольшее количество наград.
Усложним эту игру тем, что у нас есть несколько колод различного уровня сложности:
Есть колода с простыми вопросами, наградой за ответ на которые будет условная игровая фишка «Монета». Назовем эту колоду «Зеленой».
Есть две колоды с вопросами средней сложности, наградой за которые будет «Свиток» или «Манускрипт». Назовем эти колоды «Красная» и «Синяя».
Есть одна колода с вопросами высокой сложности, наградой за которые будет «Книга». Назовем эту колоду «Золотой».
Игроки ходят по очереди, и в свой ход могут взять 1 вопрос из любой колоды. При этом взять вопрос из Зеленой колоды они могут бесплатно, а чтобы взять вопрос из Красной или Синей колоды, нужно отдать Монету, полученную ранее за ответ на вопрос из зеленой колоды. Чтобы испытать удачу с картой из Золотой колоды, нужно в качестве платы отдать Свиток и Манускрипт, ранее полученные за верный ответ на вопросы из Синей и Красной колоды соответственно.
Награды за правильные ответы на вопросы (Монеты, Свитки, Манускрипты и Книги) имеют разную ценность. Побеждает игрок, который в конце игры будет обладать наградами с наибольшей суммарной ценностью.
Задача
Рассчитать какой должна быть ценность наград, чтобы в игре не было доминирующей стратегии и выбор колоды с вопросами стал дополнительной дилеммой для игрока.
Решение
Первым делом нам нужно понять в чем заключается разница в сложности вопросов в различных колодах. Проще всего определить ее как вероятность дать правильный ответ на вопрос в карточках этой колоды. На этапе разработки мы можем сделать допущение и предположительно расставить эти вероятности. На этапе тестирования игры, крайне желательно будет получить реальную статистику по доле верных ответов на вопросы.
Допустим, что шанс верно ответить на вопросы из Зеленой колоды — 80%.
Шансы ответить на вопросы из Красной и Синей колоды — 60%.
Шанс ответить на вопрос из Золотой колоды — 40%.
Теперь нам нужно определить некий базовый ресурс, который мы можем использовать в качестве основы для дальнейших вычислений. И это один из самых важных моментов в расчете баланса. Необходимо найти “точку опоры”, отталкиваясь от которой можно выстраивать все последующие закономерности. Эта точка опоры может быть как константой, так и переменной. В некоторых, более сложных ситуациях, таких точек может быть несколько и они могут быть даже косвенно или напрямую зависимы друг от друга. Главное — взять что-то за основу, и найти способ количественно оценить стоимость всех остальных ресурсов, действий, возможностей и прочих элементов через этот базовый ресурс.
В данном примере хорошим кандидатом на звание такого ресурса является ход игрока (попытка ответа на вопрос). Скорее всего игра будет ограничена количеством ходов, которые может совершить каждая команда. В случае верного ответа, ход, как ресурс, конвертируется в награду. В случае ошибки игрока — ход, как ресурс, утрачивается.
Таким образом задачей игрока является наиболее выгодный обмен попыток ответа на награды. А нашей задачи — выставление таких “курсов обмена”, при которых решающую роль будет оказывать правильность ответов на вопросы, а не грамотный выбор карточек. И, в целом, игра будет ставить перед игроком дилемму — взять вопрос попроще, или посягнуть на более сложные задачки, рискуя потерять ранее заработанные очки.
Посмотрим на Зеленую колоду. Игрок может потратить попытку, чтобы взять карточку из колоды и попытаться ответить на вопрос. Если он ответит правильно, то он получит 1 Монету. В случае неверного ответа, он не получит ничего. Допущенная нами статистика верных ответов — 80%. Это значит, что среднестатистический игрок на каждый 5 вопрос ответит неправильно. Тогда сделаем так, чтобы среднестатистический игрок мог преобразовывать попытки в награды по курсу 1 к 1, несмотря на то, что он будет периодически ошибаться. Для этого нужно назначить ценность монеты в размере 1,25.
При курсе 1 к 1 каждая попытка должна превратиться в одно очко. Если на 20% (1 из 5) вопросов среднестатистический игрок ответит неверно, то ценность награды должна быть выше настолько, чтобы компенсировать эту статистическую ошибку. Т.е. на 5 попыток и 4 верных ответа, должно получаться 5 очков. 5 делим на 4, получаем 1,25. Аналогичный результат мы получим, просто разделив 1 (стоимость попытки в ходах) на 80% (вероятность успеха).
В принципе, этот шаг можно было пропустить и назначит ценность монеты в 1, игнорируя вероятность ее получения. Но я решил сделать его, поскольку так проще будет объяснить логику последующих шагов. Да и в дальнейшем строить таблицы проще, если сохраняется единая логика для всех однородных элементов.
После того, как мы приняли ценность Монеты как 1,25, можно рассчитать ценность Свитков и Манускриптов. Стоимость попытки ответить на вопрос из Синей и Красной колоды в данном случае возрастает, поскольку помимо хода, игрок должен отдать 1 Монету, что дает нам 1 (ход) + 1,25 (ценность монеты) = 2,25. При этом только в 60% случаев получится дать верный ответ и получить в награду Свиток или Манускрипт. Если мы сохраняем целью удержать обменный курс ходов на награды 1 к 1 для среднестатистического игрока, то это потребует, чтобы ценность Свитков и Манускриптов была установлена как 3,75 (2,25 / 60% = 3,75).
Аналогично рассчитывается ценность Книги. Стоимость попытки для Золотой колоды составит 1 (ход) + 3,75 (свиток) + 3,75 (манускрипт) = 8,5. При этом успешными окажуться только 40% попыток. 8,5 / 40% = 21,25
Мы получили не самые удобные для обращения во время игры цифры ценности наград:
Монет — 1,25
Свиток — 3,75
Манускрипт — 3,75
Книга — 21,25
Однако никто не мешает нам принять ценность монеты за 1, и относительно это ценности подправить все остальные награды, просто разделив их ценность на 1,25:
Монета: 1,25 / 1,25 = 1
Свиток: 3,75 / 1,25 = 3
Манускрипт: 3,75 / 1,25 = 3
Книга: 21,25 / 1,25 = 17
При текущем балансе, для среднестатистического игрока неважно из какой колоды брать карточки. В среднем, в любом случае он будет получать один и тот же результат.
Игроку, способному ответить правильно на большее количество вопросов, чем предусмотрено статистикой, выгодно рисковать и сосредоточиться на получении Книг.
Игроку, чьи познания не позволяют отвечать на уровне среднестатистического игрока, выгоднее сосредоточиться на Зеленой колоде, так как пытаясь ответить на более сложные вопросы он больше потеряет, чем приобретет.
Это добавляет интереса игре, поскольку помимо тактических ответов на вопросы, появляется стратегическая задача грамотной оценки своих сил и возможностей.
Однако вспомним, что параметры среднестатистического игрока мы взяли “с потолка”. Что же делать, если нам нужно их изменить или скорректировать? Тут на помощь приходит балансировочная таблица.
Таблица
Готовая таблица для данного примера находиться по ссылке.
Тут же я объясню ее устройство, понимание которого (в сумме с базовыми навыками обращения с электронными таблицами) позволит самостоятельно создавать подобные таблицы и для других ситуаций.
Данная таблица сделана так, чтобы с помощью нее можно было рассчитывать баланс для любой игры с использованием указанной выше механики.

В первом столбце «Ресурс» указывается название ресурса (награды), для нашего удобства.
В следующем столбце «Код» указывается некий уникальный идентификатор для каждого ресурса. Он потребуется для дальнейшего нахождения нужного ресурса с помощью формул.
«Стоимость попытки» будет вычисляться с помощью формулы, которую подробно разберем позднее.
«Ценность в очках» — это искомые нами значения. Первая ячейка в данном столбце имеет зеленый цвет и в ней можно задавать стоимость в очках для одного из ресурсов (который будет считаться базовым, в нашем примере это «Монета»). Ценность остальных ресурсов вычисляется относительно этой ячейки.
«Вероятность успеха» — это те самые вентили, подкручивая которые, мы можем настраивать игровой баланс. По своему желанию мы можем изменять значения, задавая требуемый нами уровень “среднего игрока” или устанавливать их согласно реально собранной статистике.
«Базовая временная стоимость» — столбец, который позволяет дополнительно усложнить механику, сделав так, что взятие карточек из определенных колод будет требовать, например, 2 хода. А из некоторых, наоборот, можно будет брать по 2 и более карточек за ход.
В столбце «Дополнительная временная стоимость» суммируется временная стоимость всех ресурсов, которые нужно отдать за взятие карточки из колоды.
В группе столбцов «Коды требуемых ресурсов» как раз выставляются коды ресурсов, которые требуются для попытки ответа, и которые указаны для ресурсов в столбце “Код”. В данном варианте эта таблица позволяет указывать до 6 различных ресурсов в качестве платы за попытку. При этом можно указывать одинаковые ресурсы.
В группе столбцов «Стоимость требуемых ресурсов» собирается информация о временной стоимости каждого из ресурсов, указанного в качестве платы.
Теперь о принципе работы. Я предпочитаю использовать таблицы Google Sheets или LibreOffice (Open Office), но все тоже можно реализовать в Excel от Microsoft, правда названия функций немного измениться.
С помощью функции VLOOKUP каждая ячейка в группе столбцов «Стоимость требуемых ресурсов» находит значение временной стоимости ресурса, код которого был указан в аналогично расположенной ячейке группы столбцов “Коды требуемых ресурсов”.
С помощью функции SUM все полученные значения в группе столбцов «Стоимость требуемых ресурсов» складывается и отображается в ячейке «Дополнительная временная стоимость».
Далее с помощью базовых арифметических операций для каждой строки складываются значения «Базовой временной стоимости» и «Дополнительной временной стоимости», полученная сумма делиться на “Вероятность успеха” и результат отображается в столбце “Стоимость попытки”.
Во избежании отображения сообщений об ошибках (например деления на 0), в некоторых формулах с помощью функции IF выставлена проверка на ненулевые значения в ячейках.
Чтобы вычислить ценность ресурса в очках, сопоставимое с тем, что было назначено в ячейке «Ценность» для первого ресурса, значение столбца «Стоимость попытки» разделяется на произведение «Стоимости попытки» и «Ценности» базового ресурса.
Применение таблицы и механики
Роман Крылов, познакомившись с данным примером, показал как его можно использовать и в других метафорах.
Он предложил вариант игры, в которой по тем же самым принципам, игрок выступает в роли владельца рабов-гладиаторов в Древнем Риме. Колоды с карточками становятся аренами, куда можно отправлять своих гладиаторов; награды — статусами гладиатора и показателями его опыта и умений; вероятность успеха — шансами гладиатора на выживание и победу в поединках.
Аналогичным образом, можно использовать данную механику (и, соответственно, балансировочную таблицу для нее) в создании других игр.