В настольных и кабинетных играх для генерации случайных чисел зачастую используются игральные кубики. Однако часто для разработки сбалансированной игры требуется получить более сложные распределения случайных величин, чем линейное, задаваемое одной игральной костью. Более того, порой требуется задать распределение в определенных числовых рамках и точно знать, какова вероятность выпадения того или иного значения.
Чтобы упростить себе разработку и балансировку игр в вышеописанных ситуациях, я в свое время создал для себя небольшую шпаргалку. Думаю, что такая подсказка может пригодиться как начинающим разработчикам, так и активным игрокам. Поэтому в данной статье я поделюсь своими расчетами, а так же методом, при помощи которого можно высчитывать вероятности для любых комбинаций игральных костей.
Общая вводная
Для начала я бы хотел немного раскрыть терминологию, которая будет использована в дальнейшем.
Исторически сложилось, что бросок игральной кости обозначается как XdY, где X — количество бросков, а Y — число граней или иное маркирование типа кости. Например 1d6 означает 1 бросок 6-гранного кубика. Буква d означает dice (мн. ч. от die — игральная кость, кубик (англ.)). Закоренелые игроки так и называют игровые кости — дайсы. Впрочем, иногда встречается и русский вариант записи — 1к6. Лично я предпочитаю использовать слово дайс, поскольку «кубик» у меня строго ассоциируется с 6-гранником 🙂
Соответственно, сам дайс в такой системе обозначается как dY. Так что если вам вдруг встретится запись вида d6, знайте, что это просто 6-гранный кубик. А запись 2d10 означает «результат двух бросков 10-гранного дайса».
В качестве d2 может использоваться обыкновенная монета. Наиболее часто встречаются следующие форматы дайсов: d4, d6, d8, d10, d12, d20. Реже можно встретить d30. Особые ухищрения позволяют моделировать d100 с помощью двух d10, однако наибольшее распространение получил, конечно же, d6.
В некоторых старых компьютерных играх можно встретить такие интересные обозначения как 1d3 или 3d17. Естественно, представить себе 17-гранный кубик немного проблематично, так что, по сути дела, это — своеобразный переходный артефакт, когда компьютер уже позволял задавать случайное распределение в любом диапазоне, но игроки по старой привычке ориентировались по дайсовой схеме. В современных компьютерных играх обычно указан разброс случайных значений в формате X-Y. Например 15-85, что означает случайное значение от 15 до 85.
Впрочем, нас сейчас интересуют дайсы, так что вернемся к ним. Дайсовая форма записи имеет небольшое преимущество над записью формы X-Y. Хоть по-сути 2d6 означает случайную величину от 2 до 12, но в случае записи 2-12 нам неведом график распределения между этими значениями. Т.е. мы не знаем, одинакова ли вероятность выпадения, например 7 и 10. 2d6, в свою очередь, подразумевает не только границу значений 2-12, но и определенный порядок распределения случайных величин, о чем и пойдет речь далее.
Осталось добавить, что для смещения диапазона значений используются так называемые модификаторы броска. Фактически, это просто число, которое прибавляется или вычитается из результата броска. Записывается это в форме XdY+Z, где Z — и есть модификатор. Например, 1d6+3 означает 1 бросок 6-гранного кубика, к результату которого прибавляется 3.
С обозначениями разобрались, можно двигаться дальше.
1d6
В качестве подопытного возьмем знаменитый d6. При необходимости расчеты для любых других вариантов (включая экзотические d17) делаются без особых затруднений по аналогии. Главное — понять принцип.
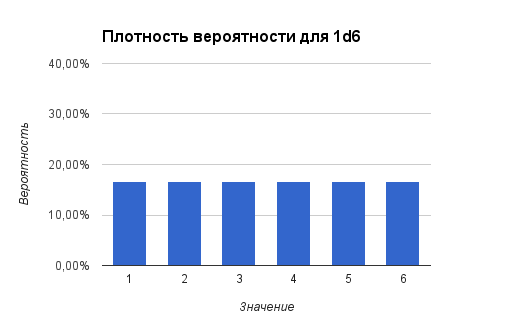
Сначала проанализируем плотность вероятностей для броска 1d6.
Плотность вероятностей в нашем случае — это шанс выпадения тех или иных значений на кубике.
Очевидно что вероятность кубика упасть на ту или иную грань, в случае когда у нас идеально сбалансированный и не крапленый кубик, обратно-пропорциональна количеству его граней. Для d6 она, соответственно, составляет 1/6 или 16,67%. Т.е. любое из 6 значений выпадает с равной вероятностью в 16,67%.
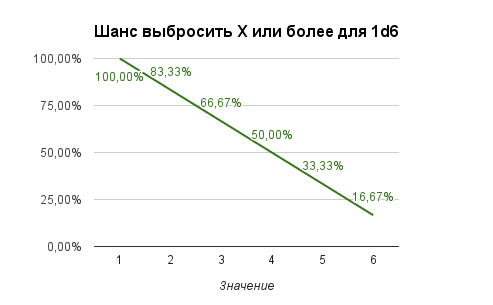
Порою весьма полезно бывает знать какова вероятность выбросить значение равное или превышающее какое-то число. Кстати, такое значение принято записывать как X+. Например, 4+ означает «4 и более». Впрочем, к обозначению 18+ уже многие привыкли, так что освоиться с такой записью не составляет никакого труда 🙂
Посчитать такую вероятность довольно просто. Достаточно просуммировать вероятности всех удовлетворяющих нас результатов. Например в случае 5+ для 1d6 нас интересует сумма шансов выбросить 5 и 6. А это 1/6+1/6=1/3 или 16,67%+16,67% = 33,33% (Все процентные значения указаны с округлением. На самом деле 16,67% это 16,666666…..6%. Поэтому не удивляйтесь тому, что иногда 7+7=13 🙂 ).
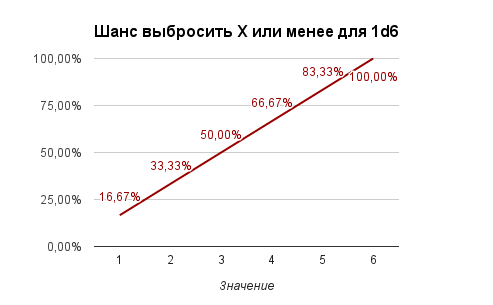
Таким образом получаем следующие графики:
Если свести все полученные данные в таблицу, то получим:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 1 | 16,67% | 1+ | 100,00% | 1 | 16,67% |
| 2 | 16,67% | 2+ | 83,33% | 2- | 33,33% |
| 3 | 16,67% | 3+ | 66,67% | 3- | 50,00% |
| 4 | 16,67% | 4+ | 50,00% | 4- | 66,67% |
| 5 | 16,67% | 5+ | 33,33% | 5- | 83,33% |
| 6 | 16,67% | 6 | 16,67% | 6- | 100,00% |
Ничего необычного. Для любого единичного броска кубика с любым количеством граней мы будем получать равномерное линейное распределение. Но что будет, если мы будем рассматривать результат нескольких бросков?
2d6
Проанализируем плотность вероятностей для 2d6. Для этого нам потребуется составить матрицу, столбцы которой будут результатами первого броска, а строки — второго.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
Теперь нам нужно высчитать вероятности всех возможных исходов при двух бросках и записать их в ячейки матрицы. Если вероятность выбросить на d6 1 равна 1/6, то вероятность получить 1 и во втором броске равна 1/6 от 1/6, то есть 1/36 или 2,78%.
Таким образом в каждой ячейке такой матрицы получаем значение 2,78%
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 2 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 3 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 4 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 5 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 6 | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
Однако если мы заполним ту же самую матрицу значениями, которые получаются в сумме двух бросков, то получим:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Из таблицы видно, что к значению 2 от броска 2d6 ведет только 1 исход, когда оба броска показали 1. В то время как получить 4 можно одним из трех исходов: 3 и 1, 2 и 2, 1 и 3. Выходит, что вероятность получить 4 при броске 2d6 равна сумме вероятностей 3 исходов, вероятность каждого из которых равна 2,78%. Получаем 2,78%+2,78%+2,78%=8,33% (помним про округление процентов).
Если составить таблицу вероятности для всех значений, получим:
| Значение | Вероятность |
|---|---|
| 2 | 2,78% |
| 3 | 5,56% |
| 4 | 8,33% |
| 5 | 11,11% |
| 6 | 13,89% |
| 7 | 16,67% |
| 8 | 13,89% |
| 9 | 11,11% |
| 10 | 8,33% |
| 11 | 5,56% |
| 12 | 2,78% |
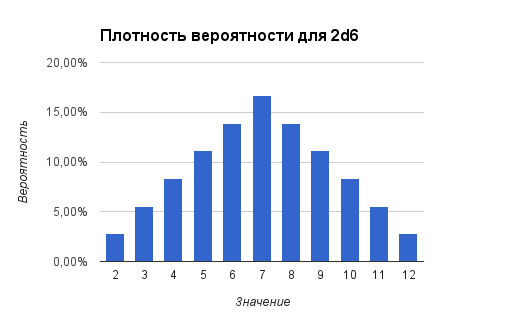
В графическом представлении это выглядит так:
Заметим, что при учете двух бросков мы получаем распределение Гаусса (оно же нормальное распределение). Вероятность получить в результате двух бросков срединное значение (в нашем случае это 7) значительно выше, чем вероятность получить крайние значения (2 или 12). Соответственно гораздо чаще результаты бросков для 2d6 будут находится среди значений 5-9 и редко показывать 2-4 или 10-12. В некоторых случаях от случайной величины требуется именно такое поведение.
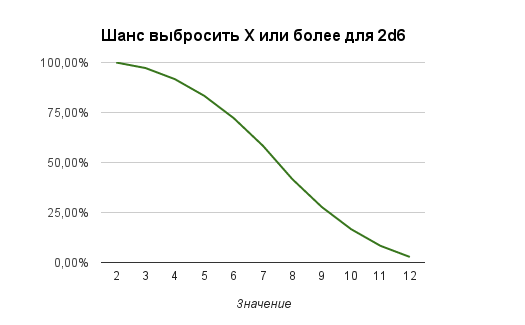
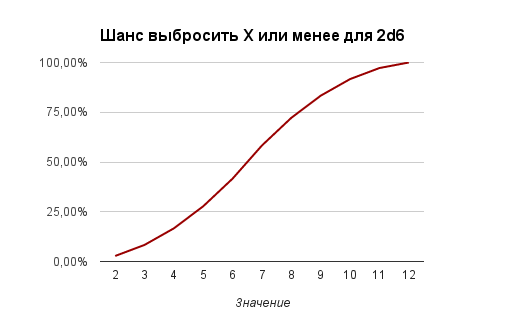
Кривые вероятности выбросить значение X+ или X- так же будут иметь нелинейный вид:
Если представить полученные данные в табличной форме, то:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 2 | 2,78% | 2+ | 100,00% | 2 | 2,78% |
| 3 | 5,56% | 3+ | 97,22% | 3- | 8,33% |
| 4 | 8,33% | 4+ | 91,67% | 4- | 16,67% |
| 5 | 11,11% | 5+ | 83,33% | 5- | 27,78% |
| 6 | 13,89% | 6+ | 72,22% | 6- | 41,67% |
| 7 | 16,67% | 7+ | 58,33% | 7- | 58,33% |
| 8 | 13,89% | 8+ | 41,67% | 8- | 72,22% |
| 9 | 11,11% | 9+ | 27,78% | 9- | 83,33% |
| 10 | 8,33% | 10+ | 16,67% | 10- | 91,67% |
| 11 | 5,56% | 11+ | 8,33% | 11- | 97,22% |
| 12 | 2,78% | 12 | 2,78% | 12- | 100,00% |
Получается, что если мы хотим получить генератор случайных чисел, который выдает распределение близкое к тому, что встречается «в природе», то использование пары кубиков или учет двух бросков дает нам эту возможность.
Ровно как и запись 2d6 имеет преимущество над 2-12 как раз в том, что указывает не только на диапазон, но и на плотность вероятностей.
Если же нам требуется получить нормальное распределение в промежутке от 0 до 10, то с помощью дайсов это можно организовать как бросок 2d6 из результата которого будем вычитать 2. Вспоминая описанные ранее обозначения, это 2d6-2.
Если такая перемена в графике произошла когда мы добавили второй бросок, то что произойдет, если ввести третий?
3d6
Для анализа плотности вероятностей для 3d6 можно, конечно составить 3-х мерную матрицу и посчитать все точь-в-точь как для 2d6. Но поскольку вероятности для 2d6 нам уже известны, то мы можем значительно упростить себе задачу:
| 2d6 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 2 | 2,78% | ||||||
| 3 | 5,56% | ||||||
| 4 | 8,33% | ||||||
| 5 | 11,11% | ||||||
| 6 | 13,89% | ||||||
| 7 | 16,67% | ||||||
| 8 | 13,89% | ||||||
| 9 | 11,11% | ||||||
| 10 | 8,33% | ||||||
| 11 | 5,56% | ||||||
| 12 | 2,78% |
Помножив вероятности результатов для 2d6 на 16,67% получим вероятности исходов для 3-х бросков:
| 2d6 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 2 | 2,78% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% |
| 3 | 5,56% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% |
| 4 | 8,33% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% |
| 5 | 11,11% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% |
| 6 | 13,89% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% |
| 7 | 16,67% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% | 2,78% |
| 8 | 13,89% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% | 2,31% |
| 9 | 11,11% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% | 1,85% |
| 10 | 8,33% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% | 1,39% |
| 11 | 5,56% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% | 0,93% |
| 12 | 2,78% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% | 0,46% |
Ну а просуммировав исходы с одинаковым результатом, получим плотности вероятностей:
| Значение | Вероятность |
|---|---|
| 3 | 0,46% |
| 4 | 1,39% |
| 5 | 2,78% |
| 6 | 4,63% |
| 7 | 6,94% |
| 8 | 9,72% |
| 9 | 11,57% |
| 10 | 12,50% |
| 11 | 12,50% |
| 12 | 11,57% |
| 13 | 9,72% |
| 14 | 6,94% |
| 15 | 4,63% |
| 16 | 2,78% |
| 17 | 1,39% |
| 18 | 0,46% |
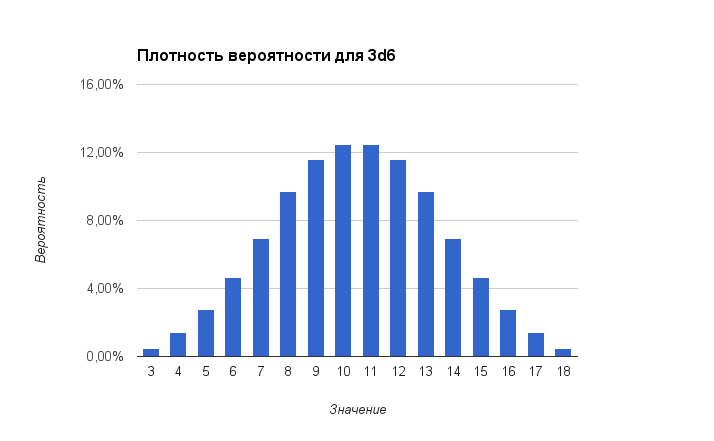
Графически это выглядит так:
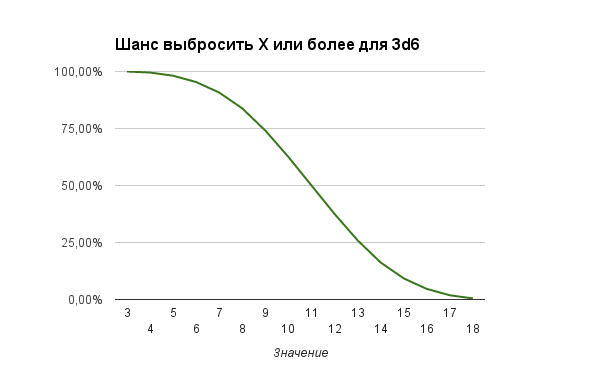
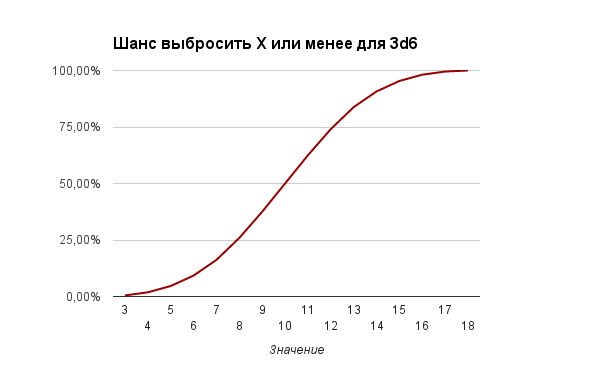
Графики вероятностей для X+ и X- тоже имеют более выраженные очертания нормального распределения:
Итоговая таблица для 3d6 будет выглядеть так:
| Значение | Вероятность | Значение | Вероятность | Значение | Вероятность |
|---|---|---|---|---|---|
| 3 | 0,46% | 3+ | 100,00% | 3 | 0,46% |
| 4 | 1,39% | 4+ | 99,54% | 4- | 1,85% |
| 5 | 2,78% | 5+ | 98,15% | 5- | 4,63% |
| 6 | 4,63% | 6+ | 95,37% | 6- | 9,26% |
| 7 | 6,94% | 7+ | 90,74% | 7- | 16,20% |
| 8 | 9,72% | 8+ | 83,80% | 8- | 25,93% |
| 9 | 11,57% | 9+ | 74,07% | 9- | 37,50% |
| 10 | 12,50% | 10+ | 62,50% | 10- | 50,00% |
| 11 | 12,50% | 11+ | 50,00% | 11- | 62,50% |
| 12 | 11,57% | 12 | 37,50% | 12- | 74,07% |
| 13 | 9,72% | 13+ | 25,93% | 13- | 83,80% |
| 14 | 6,94% | 14+ | 16,20% | 14- | 90,74% |
| 15 | 4,63% | 15+ | 9,26% | 15- | 95,37% |
| 16 | 2,78% | 16+ | 4,63% | 16- | 98,15% |
| 17 | 1,39% | 17+ | 1,85% | 17- | 99,54% |
| 18 | 0,46% | 18 | 0,46% | 18- | 100,00% |
Из полученных результатов видно, что с увеличением количества бросков до 3 «колокол Гаусса» не только сохраняется, но и становиться более выраженным. Забегая вперед скажу что и для всех последующих повышений количества бросков (4d6, 5d6, 6d6 …) эта тенденция сохраняется.
Вместо итогов
Полученные таблицы можно использовать для балансировки вероятностных значений в разрабатываемых играх. Ровно как можно с помощью данных расчетов более точно оценивать свои шансы на исход броска во время игры.
Продемонстрированный метод применим для получения таблиц к любому количеству бросков любых дайсов.
Кстати, с помощью разнообразных дайсов можно задавать довольно большой диапазон случайных значений. Например 2d6+1d4 даст нормальное распределение в диапазоне 3-16. А с помощью двух d10 можно задать линейное распределение 0-99, для этого один кубик должен отвечать за десятки, другой — за единицы. Такую комбинацию двух d10 называют «процентником».
Надеюсь, эти таблицы будут Вам полезны.